minzzl
깊이 우선 탐색 DFS (Depth-First Search) 본문
안녕하세용
오늘은 깊이 우선 탐색과 넓이 우선 탐색에 대해 공부해볼텐데요,
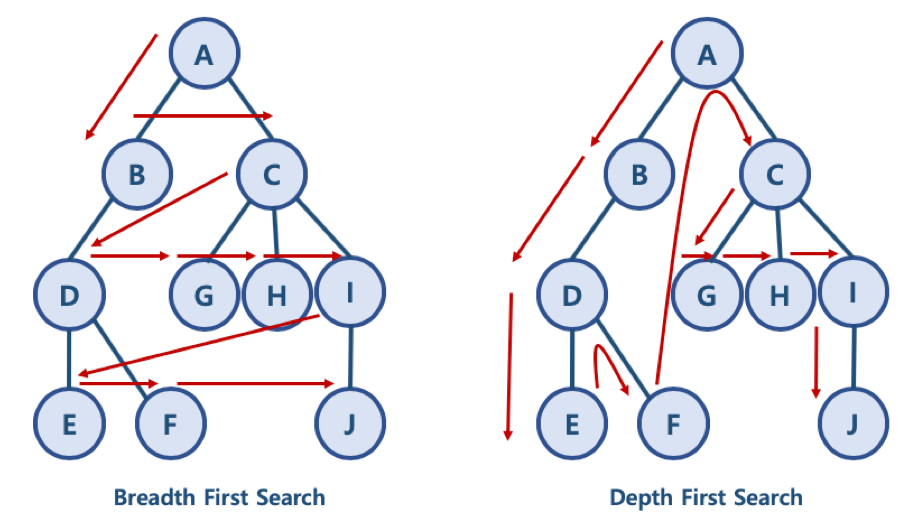
우선 깊이 우선 탐색입니당
그래프 탐색
- 하나의 정점으로 부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지
깊이 우선 탐색(DFS, Depth-First Search)
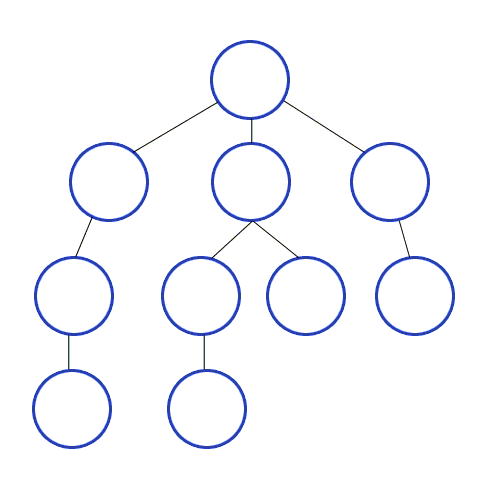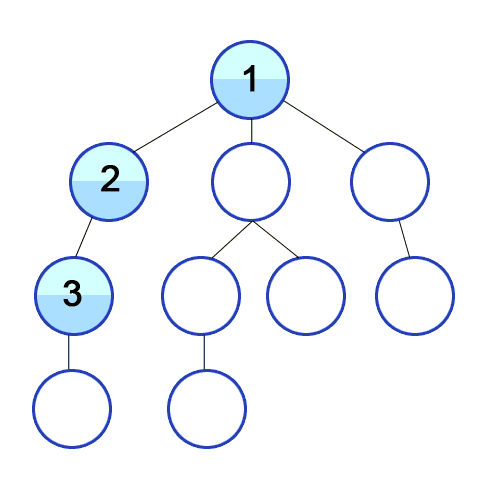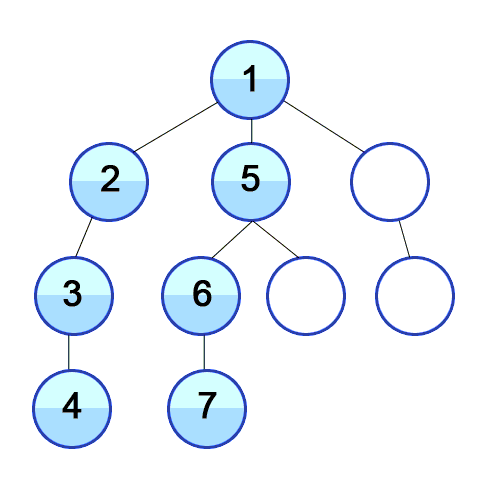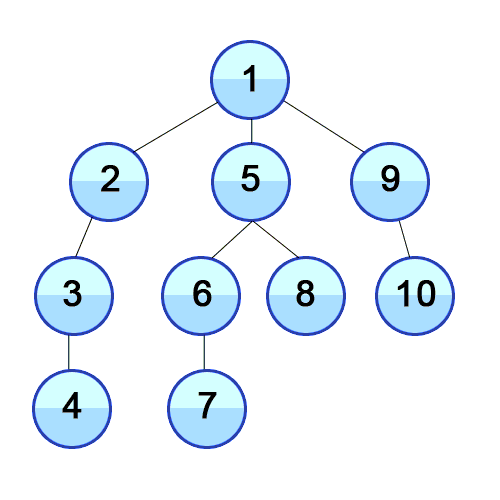
깊이 우선 탐색이란
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하기 탐색하는 방법
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
- BFS는 넓게 탐색한다면, DFS는 깊게 탐색한다.
- DFS를 사용하는 경우는 모든 노드를 방문하고자 하는 경우 이 방법을 선택한다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
깊이 우선 탐색의 특징
- 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있따.
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
- 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것이다. (이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.)
언제 사용하면 좋을까요?
- 미로 찾기
- 그래프의 위상 정렬
- 모든 경우 다 해보기(전체 탐색)
- 연결 구성 요소 찾기
- 이분 그래프
깊이 우선 탐색의 과정
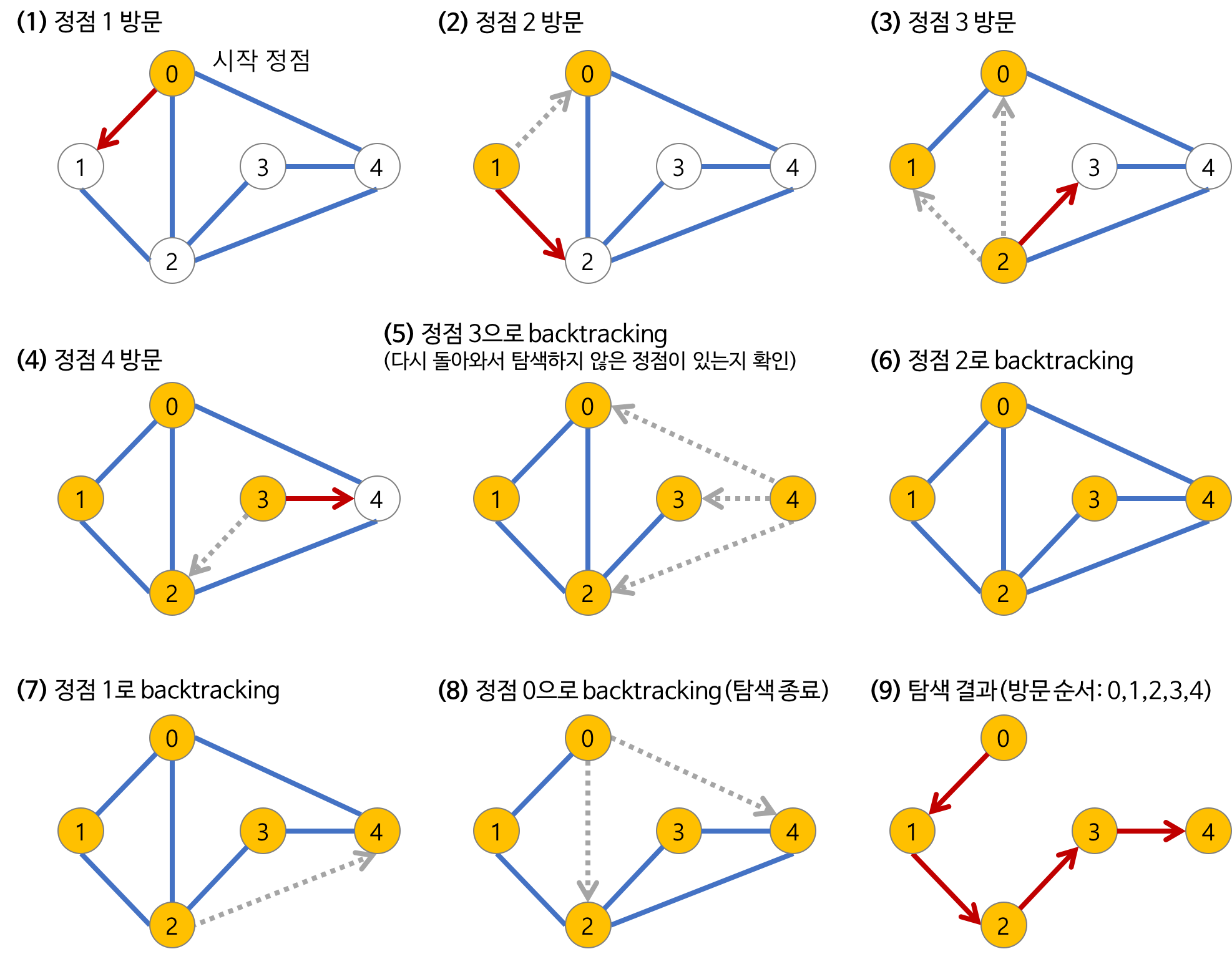
- a 노드(시작 노드)를 방문한다. 또한 방문한 노드는 방문했다고 표시한다.
- a와 인접한 노드들을 차례대로 순회한다. a와 인접한 노드가 없다면 종료한다.
- a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야한다. 즉 b를 시작정점으로 DFS를 다시 시작하여 b의 이웃노드들을 방문한다.
- b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문 할 수 있다는 뜻이다. 모든 노드를 방문했을 경우 종료한다. 있으면 다시 그 정점을 시작으로 DFS를 시작한다.
깊이 우선 탐색의 구현
DFS 에서 데이터를 찾을 때는 항상 "앞으로 찾아야할 노드" 와 "이미 방문한 노드"를 기준으로 데이터를 탐색합니다.
구현 방법 2가지
1. 순환 호출 이용
def dfs(graph, start, visited = []):
#데이터 추가
visited.append(start)
for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited
2. 명시적인 스택 사용 (스택을 사용하여 방문한 정점들을 스택에 저장했다가 다시 꺼내어 작업한다.)
(1) 리스트를 활용한 DFS 구현
def dfs(graph, start_node):
#기본은 항상 두개의 리스트를 별도로 관리 해주는 것
need_visited, visited = list(), list()
#시작 노드 지정해주기
need_visited.append(start_node)
#만약 아직도 방문이 필요한 노드가 있다면
while need_visited:
#그 중에서 가장 마지막 데이터를 추출(stack 구조의 활용)
node = need_visited.pop()
#만약 그 노드가 방문한 목록에 없다면
if node not in visited:
#방문 목록에 추가하기
visited.append(node)
#그 노드에 연결되 노드를
need_visited.extend(graph[node])
return visited
stack을 사용하여 이해하기 편하지만 pop() 을 활용하면 성능면에서 떨어진다는 단점이 있다.
따라서 이를 deque로도 구현가능하다.
(2) dequeu 를 활용한 DFS 구현
from collections import deque
def dfs(graph, start_node):
visited = []
need_visited = deque()
#시작 노드 설정해주기
need_visited.append(start_node)
#방문이 필요한 리스트가 아직 존재한다면
while need_visited:
#시작 노드를 지정하고
node = need_visited.pop()
#만약 방문한 리스트에 없다면
if node not in visited:
#방문 리스트에 노드를 추가
visited.append(node)
#인접 노드들을 방문 예정 리스트에 추가
need_visited.extend(graph[node])
return visited
* 방문 정보를 True False 로 표시
# DFS
# 방문 정보를 리스트 자료형으로 표현
visited =[False] * 9
# 각 노드가 연결된 정보를 리스트 자료형으로 표현 (2차원 리스트)
graph = [
[], # 1번 노드와 연결된 노드들
[2, 3, 8], # 2번 노드와 연결된 노드들
[1, 7], # 3번 노드와 연결된 노드들
[1, 4, 5], # 4번 노드와 연결된 노드들
[3, 5], # 5번 노드와 연결된 노드들
[3, 4], # 6번 노드와 연결된 노드들
[7], # 7번 노드와 연결된 노드들
[2, 6, 8], # 8번 노드와 연결된 노드들
[1, 7] # 9번 노드와 연결된 노드들
]
def DFS(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end = ' ')
for i in graph[v]:
if not visited[i]:
DFS(graph, i, visited)
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
DFS(graph, 1, visited)
* 다음의 글을 참고하여 작성하였습니다.
https://thalals.tistory.com/195
https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
https://www.google.com/search?q=%ED%8C%8C%EC%9D%B4%EC%8D%AC+dfs%EA%B5%AC%ED%98%84&oq=%ED%8C%8C%EC%9D%B4%EC%8D%AC+dfs%EA%B5%AC%ED%98%84&aqs=chrome..69i57j33i160l3.6666j0j7&sourceid=chrome&ie=UTF-8
'Algorithm > 기타 공부' 카테고리의 다른 글
| Python / Set() (0) | 2023.05.24 |
|---|---|
| Minimum Spanning Tree (MST) (2) | 2023.05.08 |
| Heap (0) | 2023.04.18 |
| 덱을 써야하는 이유? (2) | 2023.04.18 |




